Bubble blowing by the numbers
DOI: 10.1063/PT.3.3246
It’s a sunny day, and the two of us are taking a stroll in the park. Children are playing with bubble wands. We see the bubbles shimmering brightly as they float up into a clear blue sky. Because we are physicists, we couldn’t help wondering whether the physics of blowing soap bubbles had been described in the literature. Our intuition was that, like most classical capillary phenomena, the common experience of bubble blowing would have been explained centuries ago. To our surprise, we found that the formation of those ephemeral and fascinating fluid structures had not been fully investigated. That gap in the literature whetted our appetite for an understanding of soap-bubble formation and led to months of experimental investigations and modeling work that we carried out with two PhD students, Louis Salkin and Alexandre Schmit.
Bubble machine learning
Every bubble blown with a commercial wand, as in figure 1, forms under different conditions. The average film thickness is not reproducible, and it varies locally due to evaporation and gravitational drainage. Moreover, after only a few bubbles have been blown, the film’s soapy water is exhausted and the film bursts. To ensure the reliability and reproducibility of our measurements, we designed a bubble machine. In brief, gravity causes a bubble solution placed in a tank above the setup to flow along a pair of 1-m-long vertical wires. A giant film forms between the wires when they are separated to a width

Figure 1. Bubbles on the porch. Blowing bubbles with a wand is fun, but it is not amenable to precise experimentation. (Photograph by Linette Ortiz.)

Unlike the stationary films of common commercial wands, the films generated by our bubble machine flow downward at a controlled speed in the range of 1–4 m/s. In addition, we can adjust the films’ thickness between 1 µm and 5 µm. Our artificial mouth for blowing bubbles is a nozzle of radius

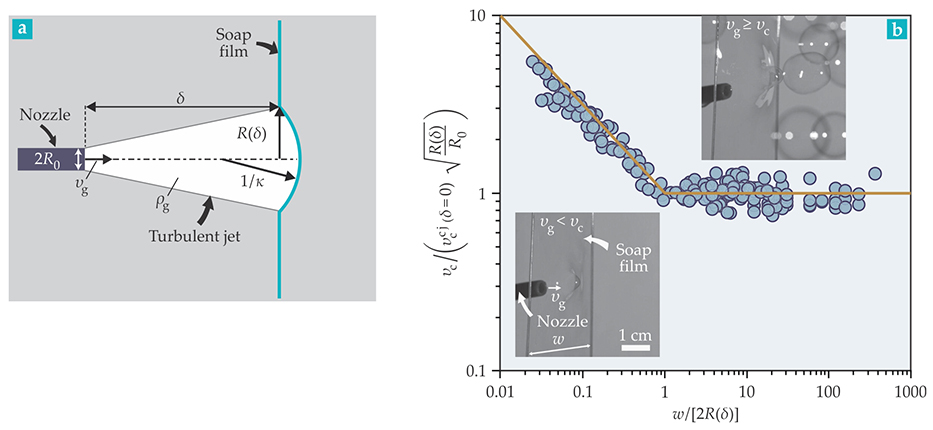
Figure 2. Bubbles in the lab. In our controlled laboratory setup, (a) a nozzle of radius
Thanks to the bubble machine, we learned that, at least under the experimental conditions we considered, neither the thickness of the film nor its downward flow velocity affects the critical speed at which bubbles form. We were glad to obtain those results because they confirmed that the bubble machine is a reasonable laboratory setup for understanding the real-world blowing of soap bubbles with stationary films that span circular wands.
Gas inertia versus surface tension
Simple dimensional analysis shows that gravitational and viscous forces are not important in our experiments; bubble formation is governed by surface tension
Our observations revealed that the shape of a dimple may be reasonably taken to be a spherical cap and that bubbles form when the radius of curvature
Real-life bubble blowing is more complicated. For one thing, a person usually blows soap bubbles at a finite distance
Before turning to velocity, we note that when a turbulent air jet penetrates air at rest, the jet assumes the shape of a cone with a universal opening angle of 23.6°. The size of the jet varies linearly with
Once turbulent fluctuations are averaged away, the gas speed has a Gaussian distribution when plotted along the direction perpendicular to the jet propagation. Given that distribution, it is a straightforward task to estimate the average gas speed
Bubbles in the classroom
The experiments described in this Quick Study can be performed in the classroom without the need for sophisticated equipment. Students would need some wire, a solution for blowing bubbles, and a caliper. The transition between dimple formation and bubble creation is visible to the naked eye, so a camera is not essential. Likewise, there is no need to purchase a flowmeter for the measurements of the gas velocity. Instead, students can simply place the gas nozzle in a burette filled with water and then turn the burette upside down and submerge it in a pool of water. They could then use a stopwatch to measure the rate
Supplemental materials
To watch dimple and bubble formation visit https://goo.gl/fTW7hV
We thank Tabby Courbin-Pancharatnam for her critical reading and useful comments.
References
1. Y. Pomeau, E. Villermaux, “Two hundred years of capillarity research,” Physics Today, March 2006, page 39. https://doi.org/10.1063/1.2195314
2. L. Courbin, H. A. Stone, “Your wetting day,” Physics Today, February 2007, page 84. https://doi.org/10.1063/1.2711652
3. Y. Couder, “Two-dimensional grid turbulence in a thin liquid film,” J. Phys. Lett. 45, 353 (1984). https://doi.org/10.1051/jphyslet:01984004508035300
4. S. B. Pope, Turbulent Flows, Cambridge U. Press (2000).
5. M. A. Rutgers, X. L. Wu, W. B. Daniel, “Conducting fluid dynamics experiments with vertically falling soap films,” Rev. Sci. Instrum. 72, 3025 (2001). https://doi.org/10.1063/1.1379956
6. L. Salkin, A. Schmit, P. Panizza, L. Courbin, “Generating soap bubbles by blowing on soap films,” Phys. Rev. Lett. 116, 077801 (2016). https://doi.org/10.1103/PhysRevLett.116.077801
More about the Authors
Pascal Panizza (pascal.panizza@univ-rennes1.fr






