A field guide to angle-independent structural color
DOI: 10.1063/PT.3.4663
“The world is blue at its edges and in its depths,” writes Rebecca Solnit in A Field Guide to Getting Lost (Penguin Books, 2005). “This blue is the light that got lost.” That comment is, on the one hand, a pithy statement about the physics of color: The ocean and sky are blue because they preferentially scatter blue light. On the other hand, it is a metaphor, and an apt one for us. While studying the physics of color, especially blue, we’ve found that it’s easy to get lost. And that is not a bad thing.
Consider the blue jay, a common sight in our home state, Massachusetts. Is it blue like the ocean or blue like the sky? In the ocean, red light is absorbed, leaving blue to be scattered back to us. In the sky, blue light is scattered more than red by the atmosphere, a process known as Rayleigh scattering. According to numerous field guides by Stan Tekiela, blue jays are like neither ocean nor sky. “Feathers lack blue pigment,” he says. “Refracted sunlight casts the blue light.”
Feather features
Wander with us while we puzzle over that explanation. It’s true that blue jays have no blue pigment. Instead, the feathers display structural color, which comes from a mechanism other than absorption (see the article by Ross McPhedran and Andrew Parker, Physics Today, June 2015, page 32
If so, it wouldn’t be the first. For most of the 20th century, Rayleigh scattering was thought to be responsible for a bird’s blue color. Because the feather’s pores are smaller than visible wavelengths, the argument goes, they should scatter more blue light than red. The isotropy of Rayleigh scattering would also explain why blue feathers, unlike iridescent opals or beetle shells, cast a structural color that depends only weakly on the viewing angle.
But constructive interference, not Rayleigh scattering, is the dominant effect in blue feathers. The matter was settled by ornithologist Richard Prum and colleagues studying another blue-colored bird, the plum-throated cotinga (figure
Figure 1.

The color of the plum-throated cotinga comes from constructive interference of blue light scattered from disordered pores in the feathers. A transmission electron micrograph of those structures in a cotinga feather is shown in the inset. (Photo by Wang LiQiang/Shutterstock.com. Inset adapted from E. R. Dufresne et al., Soft Matter 5, 1792, 2009, doi:10.1039/B902775K

A decade later, Jason Forster and colleagues at Yale University showed that when 200 nm polymer spheres aggregate, they show a similar blue. Importantly, the color appears only when the particles—proxies for the pores in the cotinga’s feathers—are densely, though randomly, packed. The results underscored the point that birdlike blues come from constructive interference.
Manipulating color
Nevertheless, Rayleigh scattering—or, more broadly, the tendency of small particles to scatter more blue light than red—can affect the color. Our research group discovered that fact during an experiment, inspired by Forster’s, when we tried to make particle packings that were red. At first the task seemed simple: Just increase the particle size, thereby redshifting the interference condition. But instead of red we got purple, a mixture of red and blue.
To make sense of that result, we developed a simple model. It assumes that light scatters just once inside the material—a crude approximation, but reasonable under certain conditions. The scattered intensity is the product of a structure factor, which describes the correlations between particles, and a form factor, which describes the scattering from individual particles (see figure
Figure 2.

(a) In the single-scattering model, the structure factor accounts for interference between waves scattered from different particles, and the form factor accounts for scattering from individual particles. The structure factor has a broad peak centered at
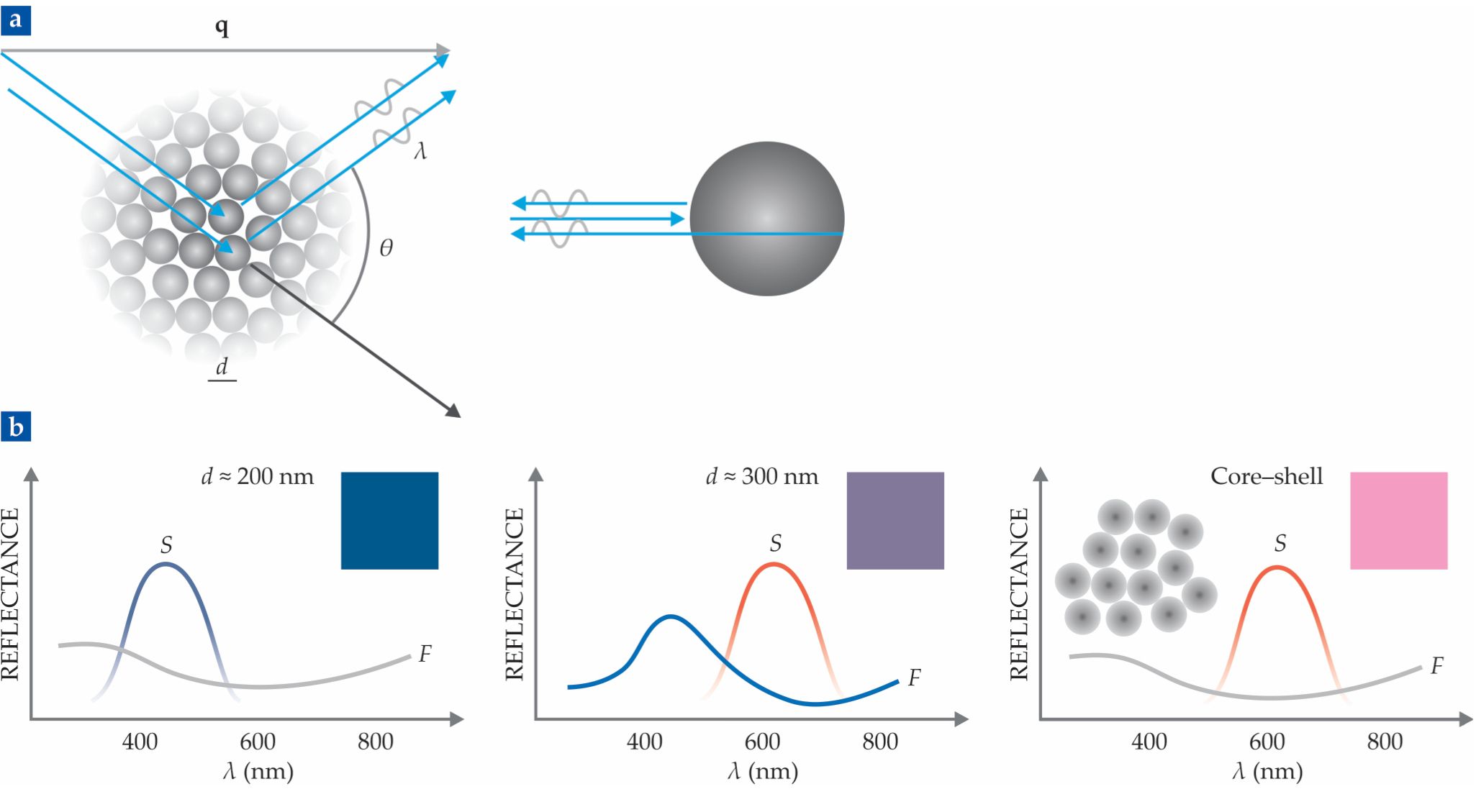
The structure factor has a broad peak centered at
The model also explains the weak dependence on the viewing angle. Our constructive interference condition is actually Bragg’s law—disguised, perhaps, by our definition of
So why did our red structural colors become purple? When the particles are 300 nm, the structure factor is peaked in the red, as expected. But the form factor has a peak in the blue (see figure
The plan worked—at least partly. The packed core–shell particles showed a reflection peak in the red and no peak in the blue. But they looked pink. That’s because light of all wavelengths can scatter more than once. Mix some of that white light with the red and you get pink. We’re now trying to reduce the multiple scattering to make a more saturated red. That might be useful for applications like reflective color displays; imagine, for example, a smartphone that is readable in direct sunlight.
Edge effects
There’s one important detail. Our model assumes that each particle is embedded in a homogeneous medium with an average, or effective, refractive index. That effective-medium approximation makes perfect sense—and can be justified by Maxwell’s equations—when the particles are tiny, as they are in a molecular mixture. It’s harder to justify when the particles are bigger, but it works well when the refractive indices don’t differ greatly.
Why is that detail important? For the model to be consistent, we must account for what happens when light hits the boundary of the effective medium. There it can reflect and—you guessed it—refract.
Stan Tekiela’s explanation wasn’t quite correct: Refraction alone doesn’t explain blue structural color. But the absence of refraction at certain angles—that is, total internal reflection—leads to some wavelengths being suppressed. And the presence of refraction alters the angular dependence of the colors that aren’t suppressed. So the guide didn’t exactly lead us astray either.
On our meandering journey, ideas that first seemed to be misconceptions—refraction and Rayleigh scattering—have become useful concepts. Like those who are lost, we go in circles. But as Rebecca Solnit writes, “Never to get lost is not to live.” Indeed, each time we circle back, we have gained new understanding.
References
► R. O. Prum et al., Nature 396, 28 (1998). https://doi.org/10.1038/23838
► J. D. Forster et al., Adv. Mater. 22, 2939 (2010). https://doi.org/10.1002/adma.200903693
► S. Magkiriadou et al., Phys. Rev. E 90, 062302 (2014). https://doi.org/10.1103/PhysRevE.90.062302
► J.-G. Park et al., Angew. Chem. Int. Ed. 53, 2899 (2014). https://doi.org/10.1002/anie.201309306
► L. Maiwald et al., Opt. Express 26, 11352 (2018). https://doi.org/10.1364/OE.26.011352
More about the Authors
Vinothan Manoharan is a professor of chemical engineering and physics and Annie Stephenson is a graduate student of applied physics at Harvard University’s John A. Paulson School of Engineering and Applied Sciences in Cambridge, Massachusetts.






