Singular Limits
DOI: 10.1063/1.1485555
Biting into an apple and finding a maggot is unpleasant enough, but finding half a maggot is worse. Discovering one-third of a maggot would be more distressing still: The less you find, the more you might have eaten. Extrapolating to the limit, an encounter with no maggot at all should be the ultimate bad-apple experience. This remorseless logic fails, however, because the limit is singular: A very small maggot fraction (f ≪ 1) is qualitatively different from no maggot (f = 0). Limits in physics can be singular too—indeed they usually are—reflecting deep aspects of our scientific description of the world.

In physics, limits abound and are fundamental in the passage between descriptions of nature at different levels. The classical world is the limit of the quantum world when Planck’s constant h is inappreciable; geometrical optics is the limit of wave optics when the wavelength λ is insignificant; thermodynamics is the limit of statistical mechanics when the number of particles N is so large that 1/N is negligible; mechanics of a slippery fluid is the limit of mechanics of a viscous fluid when the inverse Reynolds number 1/R can be disregarded. These limits have a common feature: They are all singular—they must be, because the theories they connect involve concepts that are qualitatively very different. As I explain here, there are both reassuring and creative aspects to singular limits. And by regarding them as a general feature of physical science, we get insight into two related philosophical problems: how a more general theory can reduce to a less general theory and how higher-level phenomena can emerge from lower-level ones.
The coherence of our physical worldview requires the reassurance that, singularities notwithstanding, quantum mechanics does reduce to classical mechanics, statistical mechanics does reduce to thermodynamics, and so on, in the appropriate limits. We know that when calculating the orbit of a spacecraft (and indeed knowing that it has an orbit) we can safely use classical mechanics, rather than having to solve the Schrödinger equation. An engineer designing a bridge can rely on continuum elasticity theory, without needing to know the atomic arrangements underlying the equation of state of the materials used in the construction. However, getting these reassurances from fundamental theory can involve subtle and unexpected concepts.
Perhaps the simplest example is two flashlights shining on a wall. Their combined light is twice as bright as when each shines separately: This is the optical embodiment of the equation 1 + 1 = 2. But we learned from Thomas Young almost exactly two centuries ago that this mathematics does not describe the intensity of superposed light beams: To account for wave interference, amplitudes must be added, and the sum then squared to give the intensity. This involves the phases of the two waves, ±ϕ say, and gives the intensity as |exp(iϕ) + exp(−iϕ)|2 = 2 + 2 cos 2ϕ, which can take any value between 0 and 4. So, what becomes of 1 + 1 = 2? Young himself, responding to a critic who claimed that the wall should be covered with interference fringes, agreed, but pointed out that “the fringes will demonstrably be invisible … a hundred … would not cover the point of a needle.” Underlying this explanation is a singular limit: The unwanted cos 2ϕ does not vanish but oscillates rapidly. If the beams make an angle θ, the fringe spacing is λ/2θ, vanishing in the geometrical limit of small λ. The limit is singular because the cosine oscillates infinitely fast as λ vanishes. Mathematically, this is an essential singularity of a type dismissed as pathological to students learning mathematics, yet here it appears naturally in the geometrical limit of the simplest wave pattern.
Young’s “demonstrable” invisibility requires an additional concept, later made precise by Augustin Jean Fresnel and Lord Rayleigh: The rapidly varying cos 2ϕ must be replaced by its average value, namely zero, reflecting the finite resolution of the detectors, the fact that the light beam is not monochromatic, and the rapid phase variations in the uncoordinated light from the two flashlights. Only then does 1 + 1 = 2 apply—a relation thus reinterpreted as a singular limit.
Nowadays this application of the idea that the average of a cosine is zero, elaborated and reincarnated, is called decoherence. This might seem a bombastic redescription of the commonplace, but the applications of decoherence are far from trivial. Decoherence quantifies the uncontrolled extraneous influences that could upset the delicate superpositions in quantum computers. And, as we have learned from the work of Wojciech Zurek and others, the same concept governs the emergence of the classical from the quantum world in situations more sophisticated than Young’s, where chaos is involved. For example, the chaotic tumbling of Saturn’s satellite Hyperion, regarded as a quantum rotator with about 1060 quanta of angular momentum, would, according to an unpublished calculation by Ronald Fox, be suppressed in a few decades by the discrete nature of the energy spectrum. However, nobody expects to witness this suppression, because Hyperion is not isolated: Just one photon arriving from the Sun (whose reemission enables our observations) destroys the coherence responsible for quantization in a time of the order of 10−50 seconds, and reinstates classicality. 1 Alternatively stated, decoherence suppresses the quantum suppression of chaos.
Other reassurances are equally hard to come by. For example, formally obtaining thermodynamics from statistical mechanics involves applying the mathematical saddle-point method to an infinite-dimensional integral. But although such reassurances about the appropriate application of earlier, less general theories are welcome, they look backward rather than forward. However, there is a creative side to singular limits: They lead to new physics. For large N, where a central idea is symmetry-breaking, this creative side is concisely expressed in Philip Anderson’s celebrated phrase: More is different. 2 The vast literature on critical phenomena reflects the fact that the large-N limit of statistical mechanics is singular at a critical point because there the continuum postulated in the thermodynamic limit is never reached, even when averaging over distances far exceeding the spacing between atoms. Correlations span arbitrarily large distances, and the critical state—the new physics—is a fractal. The zero-viscosity limit of fluid mechanics is singular because of the still-mysterious phenomenon of turbulence, whose definitive understanding would earn one of the Clay Foundation’s $1 million prizes.
In quantum mechanics (and indeed the physics of waves of all kinds), a range of new phenomena lurk in the borderland with classical mechanics. High-lying energy levels display remarkable universality: Their statistics depend only on whether the corresponding classical orbits are regular or chaotic, and on certain global symmetries. In the chaotic case (see the column “Quantum Chaos and the Bow–Stern Enigma” by Daniel Kleppner, Physics Today, August 1991, page 9
New ideas in physics often inspire, or are inspired by, new ideas in mathematics, and singular limits are no exception. Underlying critical phenomena is the renormalization group, which determines how systems transform, or remain invariant, under changes of scale—a fertile idea that is essentially mathematical but whose foundations have not been rigorously established. The quantum-classical connection involves divergent infinite series (for example, in powers of h), and the divergence can be traced precisely to the singularity of the limit. Some quantum phenomena involving divergent series are nonclassical reflection above a smooth potential barrier, weak quantum transitions caused by slowly varying external forces, and the representation of spectra in terms of classical periodic orbits. Mathematicians long regarded divergent series with suspicion; in 1828, Niels Henrik Abel wrote that they “are an invention of the devil, and it is shameful to base on them any demonstration whatsoever.” But such series are often the best (even the only) way to calculate physical quantities, and applied mathematicians, disregarding Abel’s censure, have freely developed sophisticated manipulations and regularizations of the divergences. An elementary example of a divergent series is 1 + 2 + 3 + 4 + …, which can be resummed to give the value−1/12; this looks like a joke, but is the unambiguous result of zeta function regularization, widely used in quantum field theory. Much more violent divergences arise from singular limits associated with the integrals and differential equations of physics, and have been tamed using more sophisticated methods. This is the domain of mathematical asymptotics and singular perturbation theory. In the 1990s, the long overdue beginnings of a rigorous mathematical theory were established.
Singular limits carry a clear message, which philosophers are beginning to hear: 3 The physics of singular limits is the natural philosophy of renormalization and divergent series. Perhaps they are recognizing that some problems of theory reduction can themselves be reduced to tricky questions in mathematical asymptotics—an extension of the traditional philosophical method, of argumentation based on words. Usually, we think of “applications” of science going from the more general to the more specific—physics to widgets—but this is an application that goes the other way: from physics to philosophy. One wonders if it counts with those journalists or administrators who like to question whether our research has applications. Probably not.

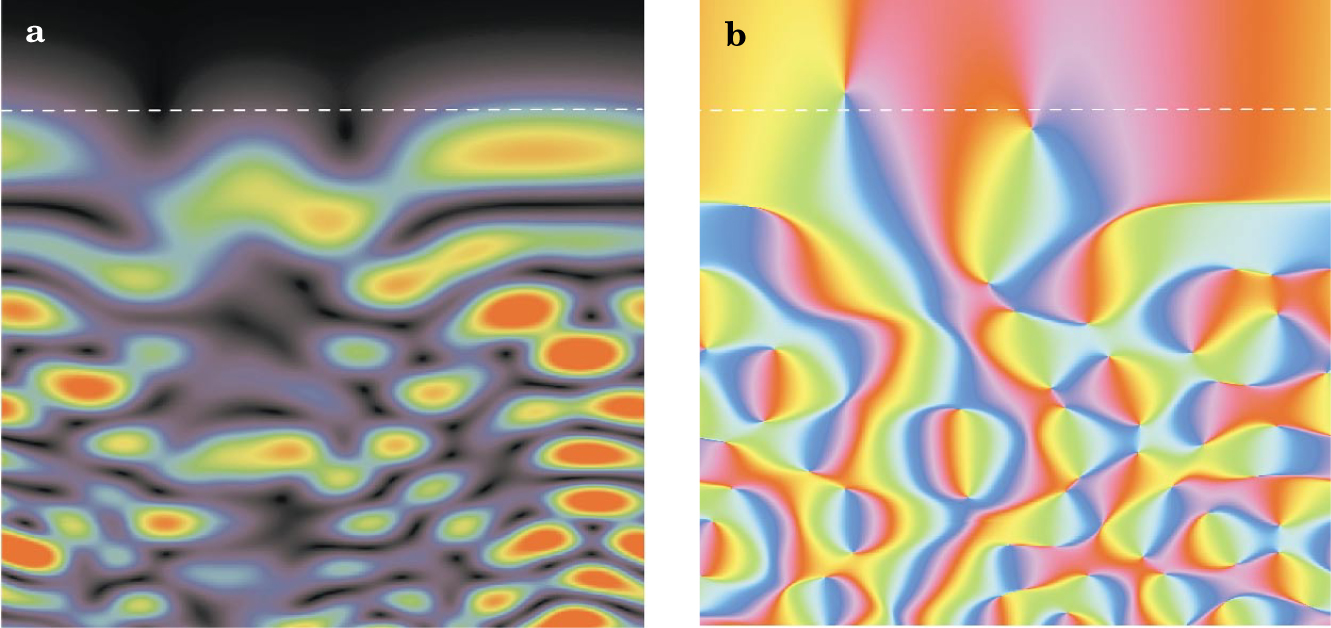
Across the boundary between classically allowed and forbidden regions in a two-dimensional chaotic system, the density of trajectories falls discontinuously to zero. This classical limit is singular because, in the corresponding semiclassical quantum wavefunctions shown here as simulations (with the classical boundary indicated by dashed lines), (a) the probability density (color-coded from red at maxima to black at zeros) fluctuates smoothly, and (b) the phase (color-coded by hue) varies smoothly except at points where all colors meet (points that are themselves singularities).
References
1. M. V. Berry, in Quantum Mechanics: Scientific Perspectives on Divine Action, R. J. Russell, P. Clayton, K. Wegter-McNelly, J. Polkinghorne, eds., Vatican Observatory Publications, Vatican City State, and The Center for Theology and the Natural Sciences, Berkeley, Calif., (2001), p. 41.
2. P. W. Anderson, Science 177, 393 (1972). https://doi.org/10.1126/science.177.4047.393
3. R. W. Batterman, The Devil in the Details: Asymptotic Reasoning in Explanation, Reduction, and Emergence, Oxford U. Press, New York (2002).
More about the authors
Michael Berry (http://www.phy.bris.ac.uk/uk/staff/berry_mv.html
Michael Berry, Bristol University, UK .




